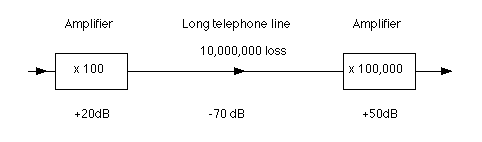
Originally proposed by Martin, W.H., "DeciBel -- the new name for the transmission unit". Bell System Tech. J. January,1929
The Decibel is a unit which is used to compare two levels of power. It is rather like a percentage, because it is comparative and does not have any absolute value.
It was originated by the telephone industry to ease the calculation of gains and losses in telephone circuits. Normally the total effect of a combination of gains and losses has to be be calculated by multiplication, but the decibel was defined as a logarithmic unit so that simple addition and subtraction could be used for the calculation.
The Bel is the logarithm (to base 10) of the ratio of two power levels. The decibel is one tenth of a Bel (which is a far more practical unit).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
When the ratio represnts a reduction, the decibels become negative:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The example below shows a long distance telephone line fed with amplified signals. At the receiving end, further amplification is needed in order to return the signal to its previous level.
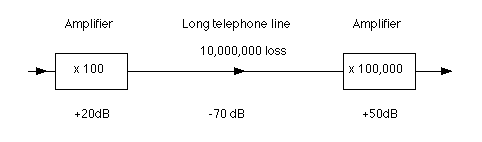
The calculation to check that there is no overall loss or gain can be done two ways:
or
When the calculations become more elaborate in a complex system, the decibel method is much easier to use.
The measurement of power is sometimes difficult or inconvenient, so another parameter is measured and the power is calculated from that measurement. In electrical work, the voltage is usually measured, and it is assumed that the power is proportional to the voltage squared. In acoustic work, the sound pressure is measured and it is assumed that the sound power is proportional to the pressure squared. The table below shows some useful ratios (approximate figures are shown in brown)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
In thses circumstances the mathematical expression for decibels is often modified to: dB = 20 Log10 (Voltage 1 / Voltage 2), but great care must be taken to ensure that this simplification is not used in circumstances where the voltage to power relationship does not hold true. For instance, decibels cannot be used to compare voltages measured in two circuits of different impedance.
The concept of decibels is so useful that it has been extended to cover other types of measurment. Sometimes the decibel is used to compare a power level with a fixed standard. In that case it is written as dBz, where the z suffix represents an agreed standard level. For example dBm is an electrical measurement of power compared with one milliwatt.
In audio work the standard level for comparison is usually the smallest sound which can be heard, but there are two suffixes in common use. In industrial noise situations, the measurements are expressed in dBA, which takes less account of low frequency sounds. This is appropriate because the majority of hearng damage results from medium and high frequency sound. Sound measurement in dBC covers equally the whole spectrum of sound within human hearing.
Footnote: If somebody expresses a sound level in decibels without specifying the standard for comparison, they are either being lazy or they are ignorant of what a decibel really is.
Various authorities differ in the detail of allowable noise exposure and the methods of measuring it; however, the table below is a fair summary of the maximum allowable levels during one working day:
|
|
|
Comments |
|
|
|
Working day exposure |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Painful |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Never to be exceeded |
|
|
|
|
|
* This is the average of the recurrent peaks, not the overall average level. |
||
Appendix "A" Section 1.
THE DECIBEL AND THE NEPER.
1. Historical,
The "Decibel" is the 1/10th part of a "bel" (after Alexander Graham
Bell, inventor of the telephone sounder), a unit in which one may
express power ratios and gain or loss ratios of related quantities such
as current and voltage. It originated in line telephony in 1923, when
the American Telephone and Telegraph Company introduced a new unit, then
called the "transmission unit"; this was to replace an older conception
based on a ratio comparison between the decrease in signal strength
produced by a given telephone line and that produced by a "mile of
standard cable." In 1924 an international advisory committee on long
distance telephony in Europe, together with the representatives of the
Bell system, agreed to recommend their countries to adopt as standards
EITHER the "bel," a unit based on logarithms to the base 10, and equal
to 10 of the American Company's "transmission units,"
OR the "neper" (after Napier), a unit based on Naperian
logarithms to the base e.
The growth in popularity of the decibel, since 1929, has been so great
that it is now almost a household word throughout all branches of
Electrical Engineering and Acoustics.
2. Definitions,
THE DECIBEL:- Two powers P1 and P2 are said to differ by N "bels" when-
P1/P2 = 10^N i.e. N=Log[10] P1/P2
4. Voltage Gain in dBs, - In general, two powers P1 and P2 will be
compared by observing either, the voltage developed across a given
impedance, or, the current through it. If the input and output
impedances of (say), an amplifier are equal, the power ratio will be
proportional to the square of the voltage or current ratio.
The voltage or current ratio relation is very frequently misused to
describe a power ratio without regard to the necessary conditions of
equality between the input and output impedance [...examples
follow...].
~~~~~~~~~~~~~